what does it mean to project one vector onto another
The dot product between two vectors is based on the project of i vector onto another. Let'due south imagine we have two vectors $\vc{a}$ and $\vc{b}$, and we want to summate how much of $\vc{a}$ is pointing in the same direction as the vector $\vc{b}$. Nosotros want a quantity that would exist positive if the ii vectors are pointing in similar directions, zero if they are perpendicular, and negative if the two vectors are pointing in nearly opposite directions. We will define the dot production between the vectors to capture these quantities.
But first, discover that the question "how much of $\vc{a}$ is pointing in the same direction as the vector $\vc{b}$" does not have anything to do with the magnitude (or length) of $\vc{b}$; information technology is based only on its direction. (Think that a vector has a magnitude and a direction.) The answer to this question should not depend on the magnitude of $\vc{b}$, just its direction. To sidestep any confusion caused past the magnitude of $\vc{b}$, let's scale the vector and then that it has length 1. In other words, allow's supersede $\vc{b}$ with the unit vector that points in the same direction as $\vc{b}$. We'll call this vector $\vc{u}$, which is defined by $$\vc{u} = \frac{\vc{b}}{\|\vc{b}\|}.$$
The dot product of $\vc{a}$ with unit vector $\vc{u}$, denoted $\vc{a} \cdot \vc{u}$, is defined to exist the projection of $\vc{a}$ in the management of $\vc{u}$, or the amount that $\vc{a}$ is pointing in the aforementioned direction as unit of measurement vector $\vc{u}$. Allow's assume for a moment that $\vc{a}$ and $\vc{u}$ are pointing in similar directions. Then, you tin imagine $\vc{a} \cdot \vc{u}$ as the length of the shadow of $\vc{a}$ onto $\vc{u}$ if their tails were together and the sun was shining from a direction perpendicular to $\vc{u}$. By forming a right triangle with $\vc{a}$ and this shadow, yous tin use geometry to summate that \brainstorm{get together}\vc{a} \cdot \vc{u} = \|\vc{a}\| \cos \theta, \label{dot_product_unit} \end{gather} where $\theta$ is the angle betwixt $\vc{a}$ and $\vc{u}$.

If $\vc{a}$ and $\vc{u}$ were perpendicular, at that place would be no shadow. That corresponds to the case when $\cos \theta = \cos \pi/2 =0$ and $\vc{a} \cdot \vc{u}=0$. If the angle $\theta$ between $\vc{a}$ and $\vc{u}$ were larger than $\pi/2$, and so the shadow wouldn't hitting $\vc{u}$. Since in this instance $\cos \theta <0$, the dot product $\vc{a} \cdot \vc{u}$ is as well negative. You could call up of $-\vc{a} \cdot \vc{u}$ (which is positive in this case) as being the length of the shadow of $\vc{a}$ on the vector $-\vc{u}$, which points in the opposite management of $\vc{u}$.
But we need to get back to the dot product $\vc{a}\cdot \vc{b}$, where $\vc{b}$ may have a magnitude dissimilar than one. This dot product $\vc{a}\cdot \vc{b}$ should depend on the magnitude of both vectors, $\|\vc{a}\|$ and $\|\vc{b}\|$, and be symmetric in those vectors. Hence, nosotros don't want to define $\vc{a}\cdot \vc{b}$ to be exactly the projection of $\vc{a}$ on $\vc{b}$; we desire information technology to reduce to this projection for the case when $\vc{b}$ is a unit vector. We tin accomplish this very easily: just plug the definition $\vc{u}=\frac{\vc{b}}{\|\vc{b}\|}$ into our dot product definition of equation \eqref{dot_product_unit}. This leads to the definition that the dot product $\vc{a} \cdot \vc{b}$, divided by the magnitude $\|\vc{b}\|$ of $\vc{b}$, is the projection of $\vc{a}$ onto $\vc{b}$. $$\frac{\vc{a}\cdot \vc{b}}{\|\vc{b}\|} = \|\vc{a}\| \cos\theta.$$ And then, if we multiply by through by $\|\vc{b}\|$, nosotros get a nice symmetric definition for the dot production $\vc{a} \cdot \vc{b}$. \begin{gather} \vc{a}\cdot \vc{b} = \|\vc{a}\| \|\vc{b}\|\cos\theta. \label{dot_product_definition}\tag{2} \end{gather}
The movie of the geometric interpretation of $\vc{a} \cdot \vc{b}$ is almost identical to the above picture for $\vc{a} \cdot \vc{u}$. We just have to retrieve that we have to divide through by $\|\vc{b}\|$ to become the projection of $\vc{a}$ onto $\vc{b}$.
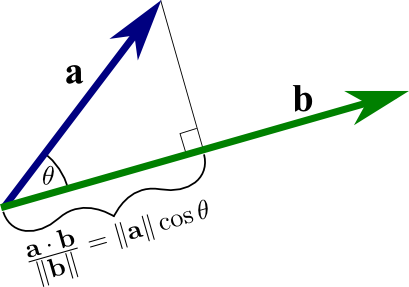
In the following interactive applet, you tin explore this geometric intrepretation of the dot product, and observe how it depends on the vectors and the angle between them. (The reported number shouldn't depend on the length of $\|\vc{b}\|$ since we divided by that magnitude.)
The dot product as projection. The dot product of the vectors $\vc{a}$ (in blue) and $\vc{b}$ (in light-green), when divided by the magnitude of $\vc{b}$, is the project of $\vc{a}$ onto $\vc{b}$. This projection is illustrated past the cherry-red line segment from the tail of $\vc{b}$ to the project of the caput of $\vc{a}$ on $\vc{b}$. Yous tin can alter the vectors $\vc{a}$ and $\vc{b}$ by dragging the points at their ends or dragging the vectors themselves. Notice how the dot product is positive for acute angles and negative for birdbrained angles. The reported number does non depend on $\|\vc{b}\|$ only because we've divided through past that magnitude.
More information about applet.
The geometric definition of equation \eqref{dot_product_definition} makes the properties of the dot product clear. One tin can run into immediately from the formula that the dot product $\vc{a}\cdot\vc{b}$ is positive for acute angles and negative for obtuse angles. The formula demonstrates that the dot product grows linearly with the length of both vectors and is commutative, i.e., $\vc{a} \cdot \vc{b} = \vc{b} \cdot \vc{a}$.
All the same, the geometric formula \eqref{dot_product_definition} is not convenient for calculating the dot product when we are given the vectors $\vc{a}$ and $\vc{b}$ in terms of their components. To facilitate such calculations, we derive a formula for the dot product in terms of vector components. With such formula in hand, we can run through examples of calculating the dot product.
Source: https://mathinsight.org/dot_product
0 Response to "what does it mean to project one vector onto another"
Post a Comment